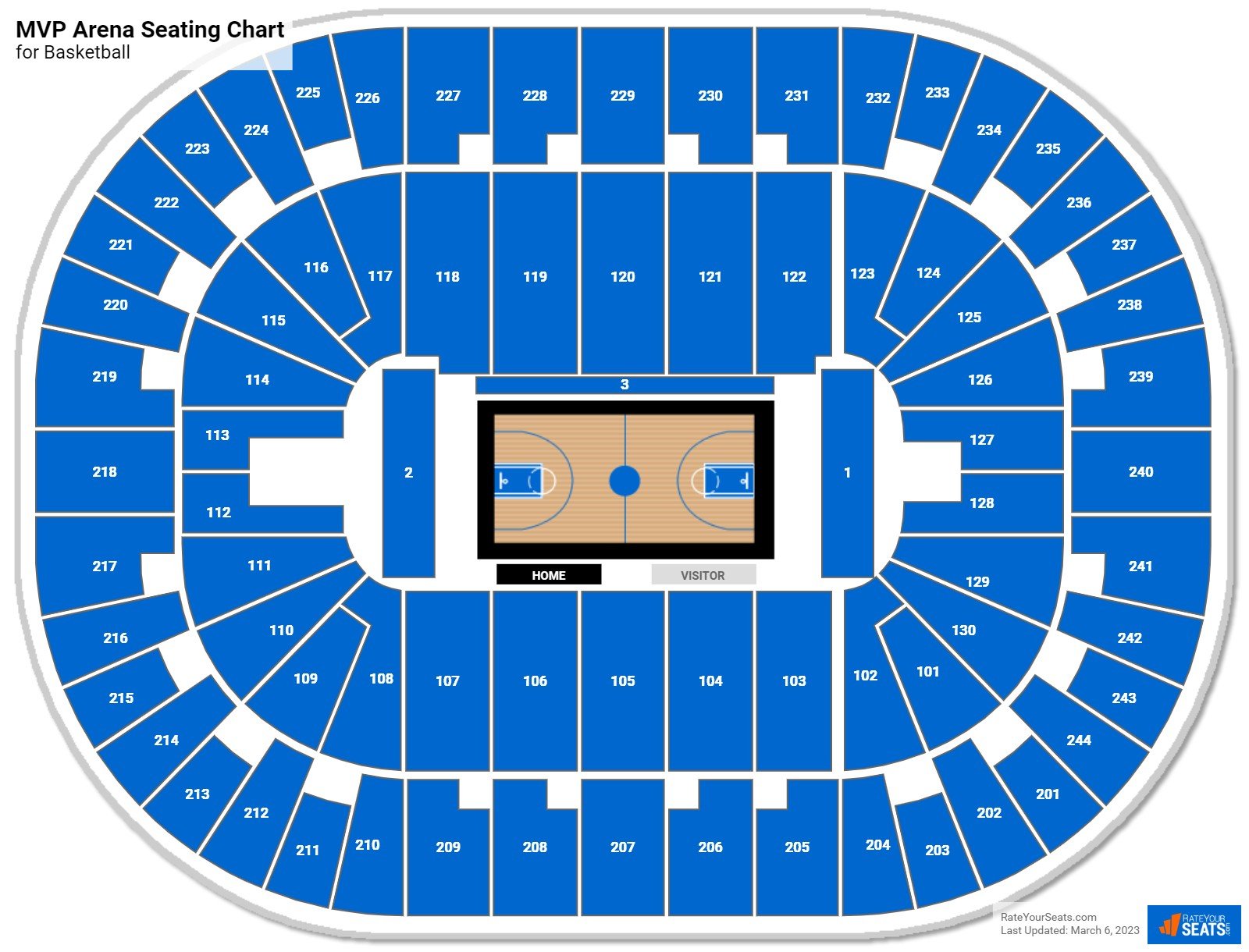
MVP Arena Basketball Seating Chart
Interactive Seating Chart
 Courtside Seating
Courtside Seating Home & Visitor Benches
Home & Visitor Benches Lower Level Seating
Lower Level Seating Upper Level Seating
Upper Level Seating
Seating Chart for Basketball
Event Schedule
- 26Apr
Jordan Davis
MVP Arena - Albany, NY
Friday, April 26 at 7:00 PM
- 3May
The Postal Service and Death Cab For Cutie
MVP Arena - Albany, NY
Friday, May 3 at 7:00 PM
- 21May
Judas Priest
MVP Arena - Albany, NY
Tuesday, May 21 at 7:30 PM
- 23May
The Avett Brothers
MVP Arena - Albany, NY
Thursday, May 23 at 7:00 PM
- 1Jun
Lauren Daigle
MVP Arena - Albany, NY
Saturday, June 1 at 7:00 PM
- 12Jun
Stevie Nicks
MVP Arena - Albany, NY
Wednesday, June 12 at 7:00 PM
- 22Jun
Ladies Love R&B
MVP Arena - Albany, NY
Saturday, June 22 at 8:00 PM
- 10Aug
Heart and Cheap Trick
MVP Arena - Albany, NY
Saturday, August 10 at 8:00 PM
- 10Sep
Megadeth
MVP Arena - Albany, NY
Tuesday, September 10 at 6:30 PM
- 24Sep
Jelly Roll
MVP Arena - Albany, NY
Tuesday, September 24 at 7:00 PM
- 3Oct
Sebastian Maniscalco
MVP Arena - Albany, NY
Thursday, October 3 at 7:30 PM
- 15Nov
MercyMe and TobyMac
MVP Arena - Albany, NY
Friday, November 15 at 7:00 PM

